From Instance Noise to Gradient Regularisation
This is just a short note to highlight a new paper I read recently:
- Roth, Lucchi, Nowozin and Hofmann (2017) Stabilizing Training of Generative Adversarial Networks through Regularization
Instance noise
Last year, we and Arjovsky & Buttou (2017) independently noticed a fundamental problem with the way GANs are trained, and proposed the same solution. The problem is, that when the support of the real data distribution $P$ and the generative model $Q$ are often non-overlapping, and in such situations the divergences we think GANs minimise are meaningless, and the discriminator can be perfect, which can lead to instabilities.
Both papers proposed adding Gaussian instance noise to both real and fake samples, essentially to blow up distributions making sure there's meaningful overlap between their supports. Another way to think about this is that we're making the discriminator's job harder. Instance noise seems to stabilize GAN training but it also a bit dissatisfying in that the sampling Gaussian noise in a very high dimensional space introduces additional Monte Carlo noise which might slow down training (although arguably I'd prefer a slow but stable training to a quicker but quasi-random process that never converges).
Analytic instance noise
What (Roth et al, 2017) propose is essentially an analytical treatment of instance noise in the f-GAN framework. As I explained in this post, instance noise can be understood as changing the divergence you use to quantify mismatch between $P$ and $Q$. If $d$ is your original divergence, instance noise changes the divergence to $d_\sigma$:
$$
d_\sigma[Q|P] = d[Q \ast\mathcal{N}_\sigma | P\ast\mathcal{N}_\sigma]
$$
[(Roth et al, 2017)] showed that, if $d$ is an f-divergence, it is possible to approximately minimise $d_\sigma$ directly without adding noise to the samples. Instead, you have to regularise the norm of certain discriminator gradients at the fake datapoints. The relationship between additive noise and gradient regularisation is not entirely surprising: it's very similar to the denoising - score matching connection, and it can be derived similarly from a Taylor approximation of the discriminator around the datapoint.
For details, and there are plenty of details I glanced over here, I recommend you read the paper. Though the maths is a bit dense, I think it's worth it.
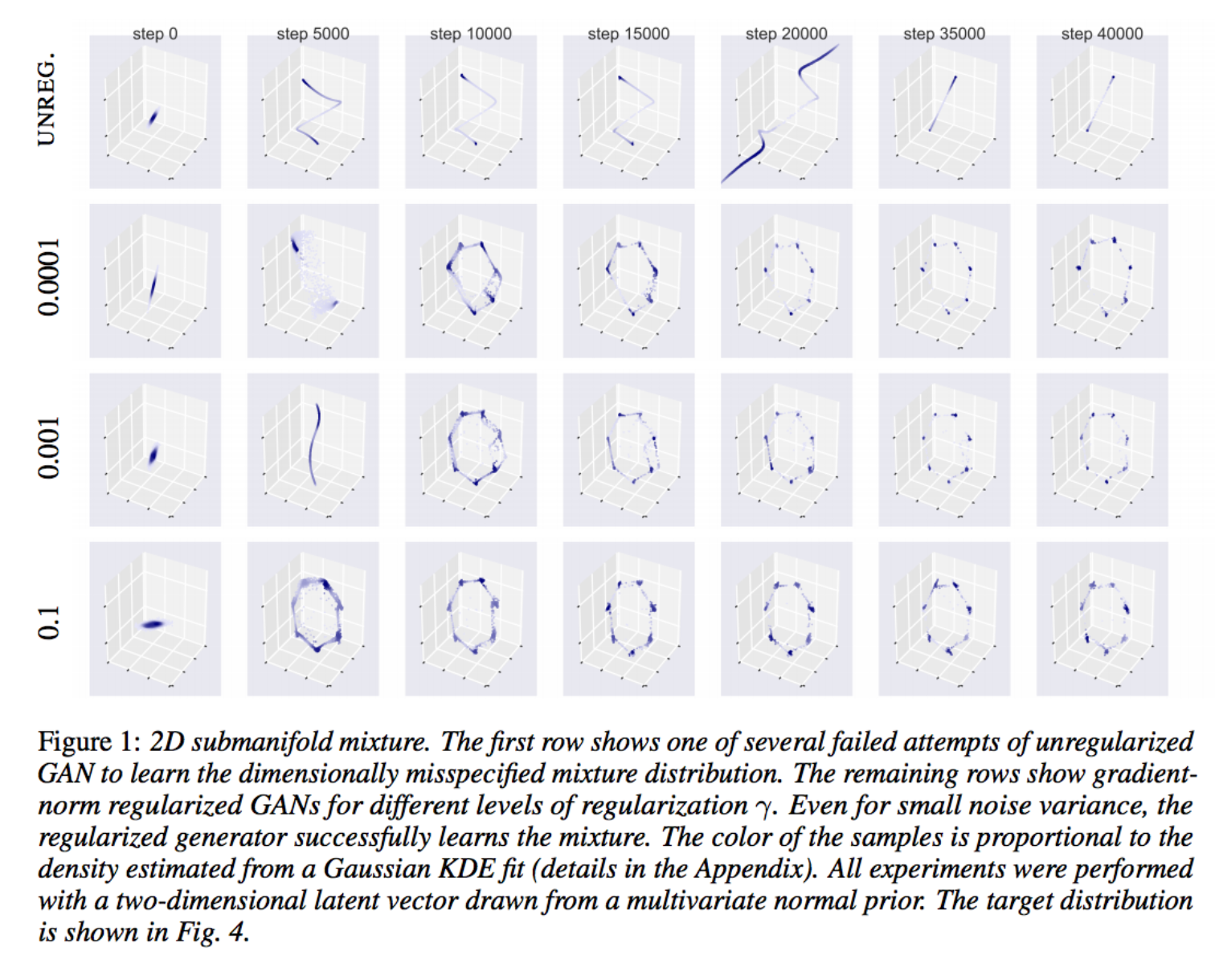
Here I just took the toy example from Figure 1 which illustrates how the regularization helps the network converge to a good solution quicker, and then stay there in a stable manner: