Sock Gnomes versus Laws of Large Numbers

Whilst finishing one of my previous posts on causality and influence, I was pairing up socks that just came out of the laundry. I was outraged to observe that, yet again, I was hardly able to pair up over half of the socks. "This cannot happen by chance, we must have sock gnomes, who deliberately mess up your socks" - I was thinking to myself. But then I realised I may be wrong, maybe it can happen by chance. Maybe it's in fact expected to happen. Perhaps I should be more surprised if I could perfectly pair up all socks. So I started looking into this problem:

Let's say we have $n$ perfectly distinguishable pairs of socks in our laundry bag. We decide to do our laundry, but because our washing machine has finite capacity, we can only wash $ k \leq 2n $ pieces of socks. We select the particular socks to be washed by drawing from the laundry bag uniformly at random, without replacement. After this procedure in our sample of $ k $ socks there will be a number $ Y_{n,k} $ of them that won't have their pairs in the sample. What is the expected value of $ Y_{n,k} $

First I wanted to give an analytic answer, but I had to many other things to use my brainpower for. So this blog post is based on random simulations and Monte Carlo estimates, that I could quickly hack together. (For those of you who doesn't know, Monte Carlo is a fancy name for simulating a bunch of random outcomes and then taking averages)

I came up with a visualisation to explain what's going on. Here's a simple (and ugly) version of plot if we have only $ n=2 $ pairs of socks, with explanation below.

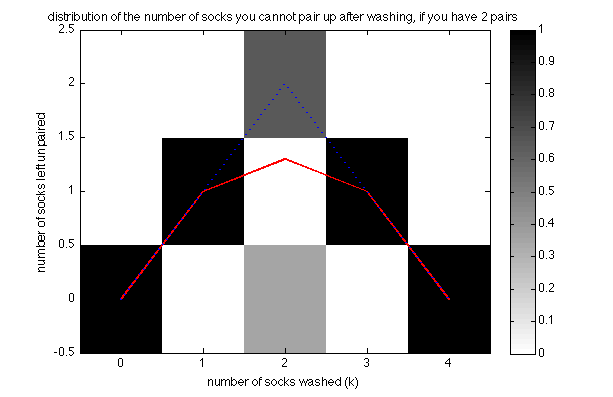
2 pairs of socks means a total of 4 pieces in our laundry bag that we may select to wash. The x axis shows the number of socks washed , $k$, which therefore ranges between $0$ and $4$. The y axis shows the number of socks left unpaired. The gray rectangles show the distribution of unpaired socks with white meaning probability $0$, black meaning probability $1$ (see colorbar on the right). Let me walk you through this figure.

• If we wash 0 socks, with probability 1 we have 0 unpaired socks, hence the black rectangle at (0,0), meaning if we wash 0 socks, with probability 1 we have 0 unpaired socks.
• If we wash a single sock, we obviously can't pair it up with anything, thus with probability one, we have 1 unpaired sock, hence the black rectangle at (1,1).
• If we wash 2 pieces, than two things can happen. With probability $\approx0.65$ those two won't be pairs of each other, so we're left with two unpaired socks, hence the dark gray rectangle at (2,2); with probability $\approx0.35$ we can actually pair them up and we're left with 0 unpaired socks, hence the lighter gray rectangle at (2,0). It's impossible to have a single unpaired sock, hence (2,1) is white.

I think by now you probably got it or left the blog. It is simple to see that graph like this will always be symmetric.

The blue dotted line shows the maximum of the number of unpaired socks, it's easy to show you can never have more than $ min(k,2n-k) $ unpaired socks. So everything above the blue dotted line should be white. The red line shows the expected number of unpaired socks as a function of $ k $, the number of pieces we have washed (remember, $ n $ is now fixed)

Let's look at a bit more complicated case. Below is the same kind of graph for the case we have $ n=10 $ pairs of socks. Notice the checkerboard-like pattern which due to the fact that the parity of the number of unpaired socks always corresponds to the parity of the number of socks washed. Pretty pleasing to the eye, isn't it?

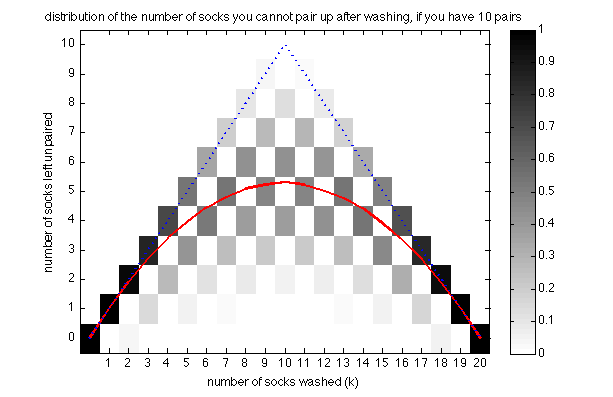
The expected number of socks starts to be a smoother function of $k$, and it becomes even smoother as we further increase this number to 50, as the following figure shows:

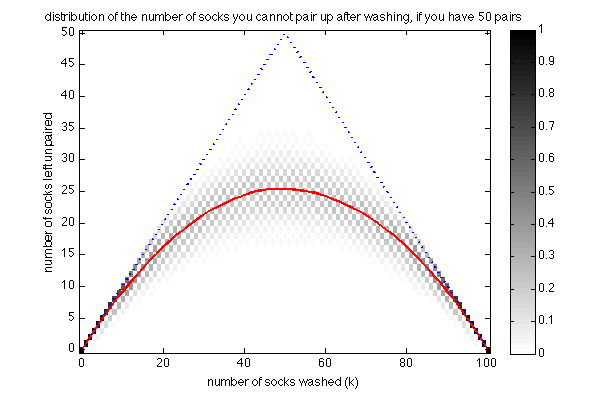
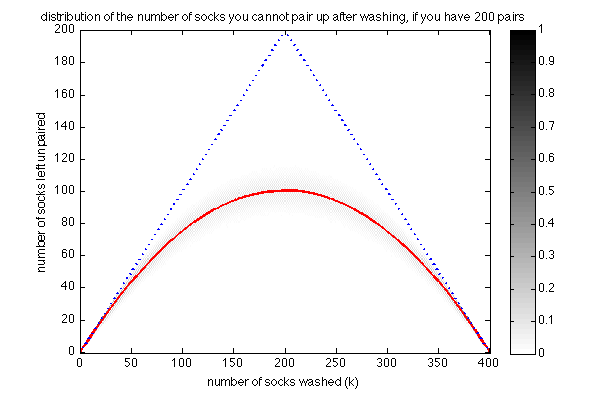
The shape of the red curve looks the same as beore, the variance around this mean however has decreased substantially. If we further increase the number of socks to 200 pairs, a law of large numbers kicks in and the variance practically shrinks to 0:

Here is a little gif putting together for growing values of $ n $:

.

So what's the answer to my frustration? Well, based on Monte Carlo simulations I conjecture that the following law of large numbers holds for sock pairing:

As $ n \rightarrow \infty$ and $ k \rightarrow \infty$ but such that $ \lambda = \frac{k}{n2}$ is fixed, the fraction of unpaired socks converges to a deterministic value with probability one:
$$\frac{Y_{n,k}}{2n} \stackrel{1}{\rightarrow} \lambda\left(1-\lambda\right) $$

So, the expected fraction of socks that you can't pair up can be as high as half of the total number of socks you have washed, so my analysis allowed me to rule out the alternative hypothesis of sock gnomes messing up my socks.

Take home message #1: Before you start believing in sock gnomes, satan, god, and other supernatural powers, check if events that seem unlikely really cannot be explained by more parsimonious models of probability.

**Take home message #2:**If you want to be able to pair up your socks, buy loads of the same colour and you won't have such problems.