Is Maximum Likelihood Useful for Representation Learning?
A few weeks ago at the DALI Theory of GANs workshop we had a great discussion about what GANs are even useful for. Pretty much everybody agreed that generating random images from a model is not really our goal. We either want to use GANs to train conditional probabilistic models (like we do for image super-resolution or speech synthesis, or something along those lines), or as a means of unsupervised representation learning. Indeed, many papers examine the latent space representations that GANs learn.
But the elephant in the room is that nobody really agrees on what unsupervised representation learning really means, and why any GAN variant should be any better or worse at it than others, whether GANs or VAEs are better for that. So I thought I'd write a post to address this, focussing now on maximum likelihood learning and variational autoencoders, but many of these things holds true for variants of GANs as well.
Latent variable models for representation learning
A common approach to unsupervised representation learning is via probabilistic latent variable models (LVMs). A latent variable model is essentially a joint distribution $p(x,z)$ over observations $x_n$ and associated latent variables $z_n$.
In any latent variable model $p(x,z)$ we can use the posterior $p(z\vert x)$ to - perhaps stochastically - map our datapoints $x_n$ to their representation $z_n$. We want this representation to be useful. The elephant in the room of course is that no-one really agrees on how to properly define, measure, let alone optimise for usefulness in the unsupervised setting. But one thing is certain: whatever our definition of the usefulness of the representation it depends on the posterior $p(z\vert x)$. As there are several joint models $p(x,z)$ with exactly the same posterior $p(z\vert x)$, there can be several LVMs whose posterior and hence representation is equally useful.
The maximum likelihood approach to training an LVM $p(x,z)$ is to maximise the log marginal likelihood $\log p(x)$ of observations. Equivalently, we can say maximum likelihood is trying to reduce the KL divergence $\operatorname{KL}[p_{\mathcal{D}}(x)|p(x)]$ between the true data distribution $p_{\mathcal{D}}$ and the model marginal $p(x)$
The problem with this is that the marginal $p(x)$ and the posterior $p(z\vert x)$ are orthogonal properties of a LVM: any combination of $p(x)$ and $p(z\vert x)$ defines a valid LVM, and vice versa, any LVM can be uniquely characterised as a $p(x)$, $p(z\vert x)$ pair. This orthogonality is illustrated in the figure below (the shading corresponds to the objective function value):
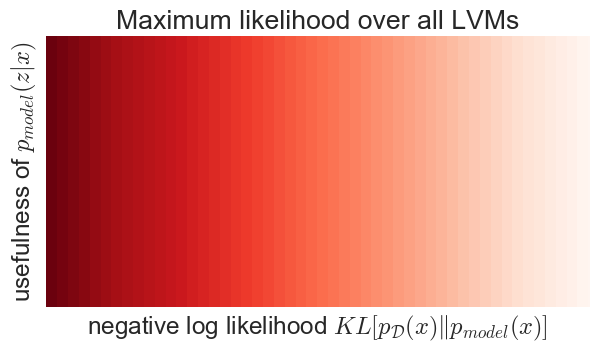
So here is the dichotomy: the usefulness of representation only depends on the y axis, $p(z\vert x)$, but maximum likelihood is only sensitive to x axis, $p(x)$. Therefore, maximum likelihood, without additional constraints on the LVM is a perfectly useless objective function for representation learning, irrespective of how you measure the usefulness of $p(z\vert x)$.
Wait, what?
So, why does it work at all? It works because you never (rarely) do maximum likelihood over all possible LVMs, you only do maximum likelihood on a parametric model class $\mathcal{Q}$ of LVMs. So let's see what happens if we do maximum likelihood with a constraint:
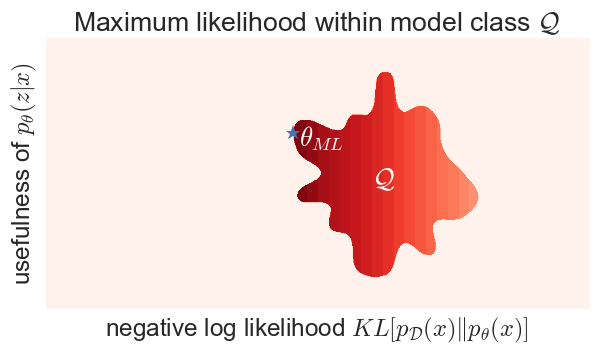
It is the structure of the model class $\mathcal{Q}$ which introduces some sort of coupling between the marginal likelihood $p_\theta(x)$ and the posterior $p_\theta(z\vert x)$. The objective function pushes you towards the left, but at some point you're squashed towards the boundary of your model class, which may push you up as well. In reality, the dimensionality of $\mathcal{Q}$ might be orders of magnitude smaller than the space of all LVMs, so this amoeba is much more likely to be some kind of nonlinear manifold. But you get the idea.
This also means that, if you choose your model-class poorly, you might be able to achieve a higher marginal likelihood, yet end up with a less useful representation:

Here, model class $\mathcal{Q}_2$ has an unfortunate shape which means you can achieve a high likelihood with a pretty useless representation.
Can this happen in practice? Sure it can. If you define a variational autoencoder-like model with Gaussian $p_\theta(z) = \mathcal{N}(0,I)$ and arbitrarily powerful $p_\theta(x\vert z)$, something like this might happen:
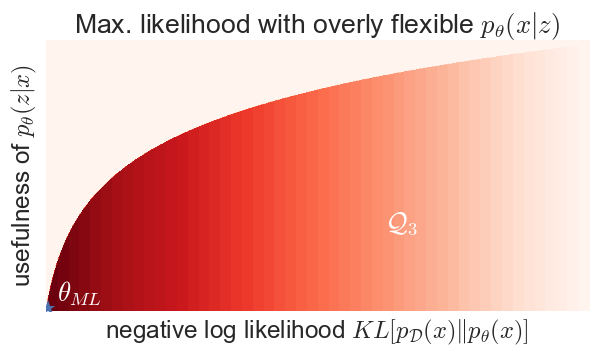
Why is this? If $p_\theta(x\vert z)$ is given arbitrary flexibility, it can in fact learn to ignore $z$ completely and always output the data distribution for each $z$: $p_\theta(x\vert z) = p_{\mathcal{D}}(x)$. Now, your LVM becomes $p(x,z) = p(z)p_{\mathcal{D}}(x)$, which has perfect likelihood, yet the posterior in this model is independent of your data so it is completely useless for representation learning. Try it, this actually happens. If you make the generator of a VAE too complex, give it lots of modelling power on top of $z$, it will ignore your latent variables as they are not needed to achieving a good likelihood.
Note on overfitting
A few commenters confused what I talked about here with the topic of overfitting. This is not overfitting. Overfitting is the discrepancy between training error and generalisation/test error. Overfitting results from the fact that although we would really like to minimise the KL divergence from the true population distribution of the data, in practice we have to estimate that KL divergence from a finite training dataset. So in essence we end up minimising the KL divergence between the empirical distribution of the training data. But overfitting is a property of how we optimise the loss function, not a property of the loss function itself.
Consider $p_{\mathcal{D}}$ which appears on my x axis to be the true, population distribution of data - not the empirical distribution of the training data. Consider my x axis to be the negative test likelihood on an infinitely large held out test/validation set which is never used for training. If we do this, we have abstracted away from overfitting, indeed, we have abstracted away from machine learning itself: there is no reference to any training dataset anymore, and I'm not even telling you how to find the optimal $\theta$, all I'm saying that models which have higher test likelihood don't necessarily provide a more useful representation.
Another way to resolve the overfitting confusion is to consider super simple LVMs with binary or discrete $x$ and $z$. If $x$ and $z$ can only take a small, finite number of values jointly, then the entire joint distribution can be represented by a joint probability table. In this case, it is not unthinkable that we can have a large enough training set that overfitting should not even be an issue at all. My argument still holds. When I say arbitrarily flexible I don't mean stupidly overparametrised neural network, I mean flexible enough to contain a large portion of all LVMs that are concievable between $x$ and $z$.
Summary
The take home message is that a good likelihood is not - by itself - a sufficient, nor a necessary condition for an LVM to develop useful representations. Indeed, whether or not a maximum likelihood LVM develops useful representations depends largely on the restrictions you place on your model class. If you let your model class be arbitrarily flexible, you can achieve a perfect likelihood without learning a representation at all. These observations are independent of how you define the usefulness of the representation, as long as you use the posterior $p(z\vert x)$ as your representation.
In practice, VAE-type deep generative models restrict the model class by fixing $p(x\vert z)$ to be Gaussian with a fixed covariance. This tends to be a useful restriction as it encourages $z$ to retain information about $x$.
Finally, the same cricitism holds for vanilla GANs as well - at least as long as we interpret of GANs as an LVM and use the posterior for representation learning. From a generative modelling perspective, GANs are very similar to maximum likelihood, but instead of minimising the KL divergence, they minimise different divergences between $p_{\mathcal{D}}$ and the marginal model $p(x)$, such as the Jensen-Shannon, reverse-KL or f-divergences. So the same figures still apply, but with the divergence on the x-axis replaced accordingly.
Variational Inference, ALI, BiGANs, InfoGANs
...stay tuned for follow-ups to this post. In the next one, I will talk about how variational learning is different from maximum likelihood. In variational learning instead of the likelihood, we use the evidence lower bound (ELBO, or - thanks to Dustin Tran - 💪). As ELBO no longer depends on $p(x)$ alone, it changes the picture slightly, maybe even for the better.
