August 4, 2016

InfoGAN: using the variational bound on mutual information (twice)

Many people have recommended me the infoGAN paper, but I hadn't taken the time to read it until recently. It is actually quite cool:

Summary of this note

Mini-review

The InfoGAN idea is pretty simple. The paper presents an extension to the GAN objective. A new term encourages high mutual information between generated samples and a small subset of latent variables $c$. The hope is that by forcing high information content, we cram the most interesting aspects of the representation into $c$.

If we were successful, $c$ ends up representing the most salient and most meaningful sources of variation in the data, while the rest of the noise variables $z$ will account for additional, meaningless sources of variation and can essentially be dismissed as uncompressible noise.

In order to maximise the mutual information, the authors make use of a variational lower bound. This, conveniently, results in a recognition model, similar to the one we see in variational autoencoders. The recognition model infers latent representation $c$ from data.

The paper is pretty cool, the results are convincing. I found the notation and derivation a bit confusing, so here is my mini-review:

$$
L_I(G,Q) = \mathbb{E}_{c\sim P(c),z\sim P(z)}[\log Q(c \vert G(c,z))] + H[c] \ldots
$$

My view on InfoGANs

I think there is an interesting connection that the authors did not mention (frankly, it probably would have overcomplicated the presentation). The connection is that original GAN objective itself can be derived from mutual information, and in fact, the discriminator $D$ can be thought of as a variational auxillary variable, exactly the same role as the recognition model $q(c\vert x)$ in the InfoGAN paper.

The connection relies on the interpretation of Jensen-Shannon divergence as mutual information (see e.g. Yingzen's blog post). Here is my graphical model view on InfoGANs that may put things in a slightly different light:

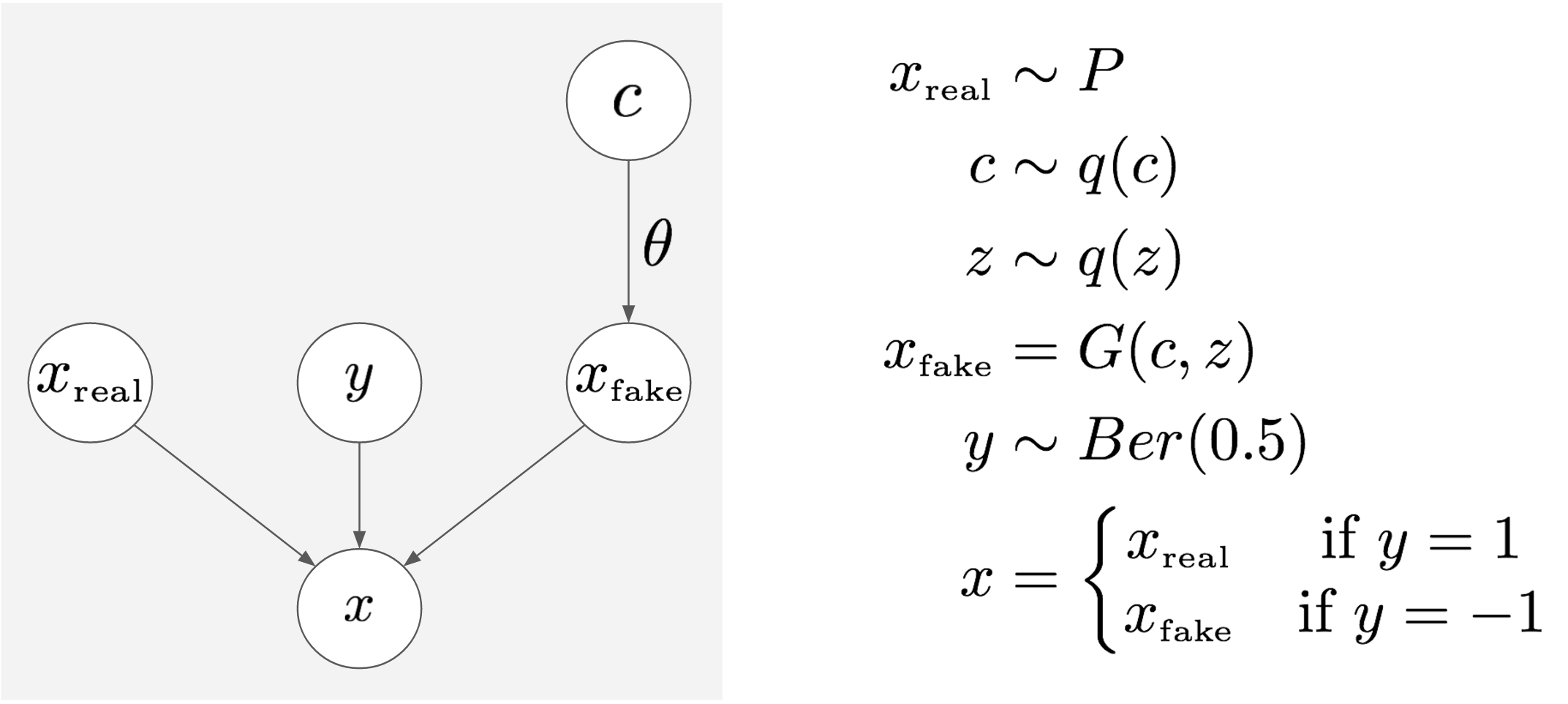
Let's consider the joint distribution of a bunch of varibles:

In this big joint distribution of all the things, everything is fixed, except for the generator's parameter $\theta$. In this world, the idealised InfoGAN loss function for $\theta$ is this:

$$
\ell_{infoGAN}(\theta) = I[x,y] - \lambda I[x_{fake},c]
$$

Just a reminder, the vanilla GAN objective would be:

$$
\ell_{GAN}(\theta) = I[x,y]
$$

The variational bound on mutual information

I think it's worth showing how one would come up with this variational bound on the mutual information. Let's say we'd like to lower bound the mutual information between two random variables $X$ and $Y$, with joint distribution $p(x,y)$:

\begin{align}
I[X,Y] &= H[Y] - \mathbb{E}_{x} H[Y\vert X=x]\\
&= H[Y] + \mathbb{E}_{x} \mathbb{E}_{y\vert x} \log p(y\vert x)\\
&= H[Y] + \mathbb{E}_{x} \mathbb{E}_{y\vert x} \log \frac{p(y\vert x) q(y\vert x)}{q(y\vert x)}\\
&= H[Y] + \mathbb{E}_{x} \mathbb{E}_{y\vert x} \log q(y\vert x) + \mathbb{E}_x \mathbb{E}_{y\vert x} \log \frac{p(y\vert x)}{q(y\vert x)}\\
&= H[Y] + \mathbb{E}_{x} \mathbb{E}_{y\vert x} \log q(y\vert x) + \mathbb{E}_{x} KL[p(y\vert x)|q(y\vert x)] \\
&\geq H[Y] + \mathbb{E}_{x} \mathbb{E}_{y\vert x} \log q(y\vert x)
\end{align}

Here, $q(y|x;\psi)$ is a parametric probability distribution was introduced as an auxillary variable. It has to be a probability distribution for the $KL$ divergence to be non-negative therefore for the bound to hold. The bound is tight if $q$ is exactly the same as the conditional distribution $p(y\vert x)$ for all $x$.

We can write this lower bound alternatively in the following way:

$$
I[X,Y] = \max_{q} \left\{H[Y] + \mathbb{E}_{x,y} \log q(y\vert x) \right\}
$$

And if we restrict $q$ to a parametric family we can say that the following lower bound holds:

$$
I[X,Y] \geq H[Y] + \max_{\psi} \mathbb{E}_{x,y} \log q(y\vert x; \psi)
$$

GANs use bound in the wrong direction!

Let's see what happens if we apply the variational lower bound on the GAN objective function above.

\begin{align}
\ell_{GAN}(\theta) &= I[x,y] \\
&\geq h(0.5) + \max_{\psi} \mathbb{E}_{x,y} \log q(y\vert x; \psi)\\
&= h(0.5) + \max_{\psi} \left\{ \mathbb{E}_{x_{real}} \log q(1\vert x; \psi) + \mathbb{E}_{x_{fake}} \log q(0\vert x; \psi)
\right\},
\end{align}

where $h(0.5) = -\log 2$ is the binary entropy function evaluated at $0.5$.

If we further expand the definition of $x_{fake}$ and rename the variational distribution to $D(x) = q(1\vert x)$, we get a more familiar loss function for GANs, similar to Equation (1) in the paper:

$$
\ell_{GAN}(\theta) + h(0.5) \geq \max_{\psi} \left\{ \mathbb{E}_{x
\sim P_{data}} \log D(x,\psi) + \mathbb{E}_{c,z} \log (1 - D(G(c,z,\theta),\psi)) \right\}
$$

Now, the main problem is with this derivation is that we were supposed to minimise $\ell_{GAN}$, so we really would like an upper bound instead of a lower bound. But the variational method only provides a lower bound. Therefore,

GANs minimise a lower bound, which I believe accounts for some of their unstable behaviour

InfoGANs use the bound twice

Recall that the idealised InfoGAN objective is the weighted difference of two mutual information terms.

$$
\ell_{infoGAN}(\theta) = I[x,y] - \lambda I[x_{fake},c]
$$

To arrive at the algorithm the authors used, one uses the bound on both mutual information terms.

  • LinkedIn
  • Tumblr
  • Reddit
  • Google+
  • Pinterest
  • Pocket