🎄 2016 Holiday Special: Deriving the Subpixel CNN from First Principles

The first paper our group published had an idea that we called sub-pixel convolution. It's a particular implementation of up-convolution that is computationally efficient to work with and seems to be easier to train via gradient descent. It works remarkably well for image superresolution:

• Wenzhe Shi, Jose Caballero, Ferenc Huszár, Johannes Totz, Andrew P. Aitken, Rob Bishop, Daniel Rueckert, Zehan Wang (2016) Real-Time Single Image and Video Super-Resolution Using an Efficient Sub-Pixel Convolutional Neural Network CVPR 2016

Though the idea is not entirely new (as we mention in the paper) this topic has gained a lot of interest and subpixel convolution kind of became a thing this year. Check out this open source iplementation for example.

What did not talk about in the paper is is why this specific architecture - ESPCN - works so well for image superresolution. Why does it outperform the previous state-of-the-art, the SRCNN (Dong et al, 2014) with the same number of parameters?

It turns out, there is a very good reason for this. This post is an argument from first principles that shows why the subpixel architecture should make a lot of sense for image superresolution. The argument applies to any inverse problem where we're trying to learn the inverse of strided convolution or spatial pooling operations, including, say JPEG artifact removal (Guo and Chao, 2016) or inverting neural activations (Zeiler and Fergus, 2013).

Start from SRCNN

The main (almost only) difference between the SRCNN and ESPCN is is where the upsampling from low-res (LR) to high-res (HR) happens. SRCNN preprocesses the data by upsampling it with bicubic interpolation. The CNN then is applied to HR featuremaps. ESPCN instead applies convolutions to the low-resolution image, and only upsamples as the very last step of the network, via a pixel shuffle/reshape operation. Both networks are trained on (LR, HR) image pairs via empirical risk minimisation trying to minimise the mean squared reconstruction error (MSE).

Let's look at the task SRCNN tries to solve. It is given a bicubic upsampled LR input $\uparrow(x^{LR}) = \uparrow(\downarrow(x^{HR}))$ and tries to infer the underlying HR input $x^{HR}$. I use $\downarrow(\centerdot)$ and $\uparrow(\centerdot)$ to denote downsampling and bicubic upsampling, respectively.

Bayes optimal behaviour

As the networks aim to minimise MSE, the best any network can ever do is to output the mean of the Bayesian posterior $p(x^{HR}\vert \uparrow(\downarrow(x^{HR})))$. We can assume that if the network is given enough data, and it is flexible enough, it can reach this Bayes-optimal behaviour.

The question then becomes representability: can our chosen neural network architecture represent the Bayes-optimal behaviour? Are there settings of parameters for which the network spits out the exact optimal thing?

Both SRCNN and ESPCN use fully convolutional neural networks (without any pooling between layers). These networks have one main assumption: they can only represent translationally equivariant functions. If you shift the input to a fully convolutional network by $p$ pixels, the output is going to be the original output shifted by $p$ pixels (except at the borders, but let's ignore those).

So is the Bayes-optimal superresolution function translationally equivariant? Let's look at the components:

• the prior specifies how likely it is that we will observe a particular HR image in the wild. As far as small translations are concerned, I think it is reasonable to expect the prior to be invariant under translations: a picture of a reindeer is about as probable as the same image picture shifted by a few pixels.
• the likelihood specifies how likely it is to observe $\uparrow(\downarrow(x^{HR}))$ given the original $x^{HR}$. In superresolution the likelihood is degenerate, as there is a deterministic mapping between the two. But is it translation-equivariant? Well, no it isn't. Let's say we perform $r\times$ downsampling using a strided convolution filter. If we shift the image by $r$ pixels either horizontally or vertically, the output of the strided convolution $\downarrow(x^{HR})$ is going to shift accordingly, and therefore the bicubic estimate $\uparrow(\downarrow(x^{HR}))$ is also going to shift by the same integer multiple of $r$ pixels. So $\uparrow(\downarrow(\centerdot))$ is equivariant to translations by $r$ pixels. But translate by a number of pixels not divisible by $r$ and $\uparrow(\downarrow(\centerdot))$ is not invariant anymore. If you don't believe it, test it. Let's call the likelihood $r$-translation-equivariant as it is only equivariant under translations by $r$ pixels.

So when you combine a largely translation-invariant prior with an $r$-translation-equivariant likelihood, you get a $r$-translation-equivariant posterior, so its mean is probably also an $r$-translation-equivariant function.

fully convolutional architectures - no matter how big or flexible - will never be able to represent the Bayes-optimal solution.

Periodically varying convolution kernels

To implement a neural network that can represent these partially translationally equivariant functions, we need to relax the weight-sharing arrangements. A normal CNN would share weights between all units in a featuremap, we now need a NN that only shares weights for units that are a multiple of $r$ pixels apart. In other words, we need $periodic weight sharing$. This operation has been called tiled convolution in (Le et al. 2010). The figure below illustrates this: units with with the same colour share the same incoming parameters.

How can we implement such spatially varying convolution efficiently? By noticing that you can write this convolution as the composition of $r^2$ normal compositions. So we can implement it as a sequence of 1 operations:

1. A space-to-channels reshape layer that reshapes the input tensor to decrease horizontal and vertical pixel count $r\times$ and increase channel count by $r^2$
2. A normal 2D convolution layer
3. A channels-to-space reshape layer that reshapes the input tensor to increase horizontal and vertical pixel count $r\times$ and decrease channel count by $r^2$.

Composing many periodic convolutions

Now, what happens when you compose a network from a series of layers like this? Notice that the channels-to-space layer one such convolution will be cancelled out by the space-to-channels operations of the subsequent layer, so you're just left with a series of LR convolution operations sandwitched between space-to-channels and a channels-to-space pixel shuffling operators.

Ultimately the bicubic $\uparrow$ operation - which is a deconvolution or up-convolution operator in itself - combines with the first space-to-channels layer, and it just becomes a fixed linear convolution layer. We can replace this with a trainable convolution layer, and we already arrived at the ESPCN architecture:

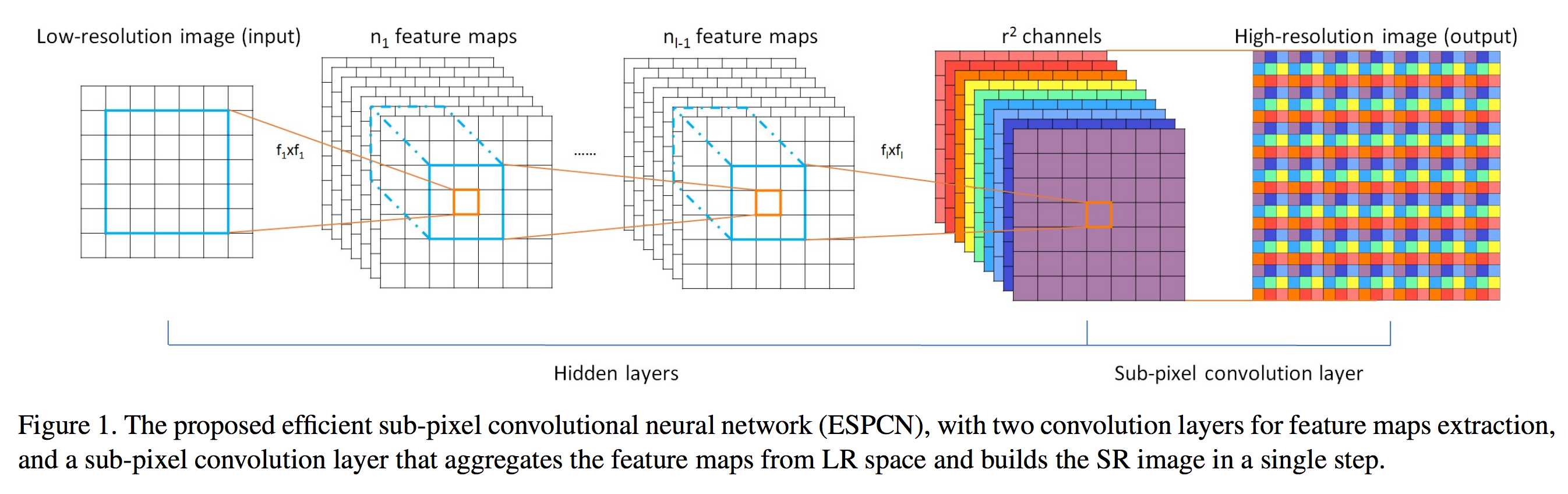
Summary

The ESPCN architecture can be derived from first principles by observing that in order to implement the optimal filtering behaviour the network has to allow for partial translational equivariance, which can be implemented as periodic weight sharing. Periodic weight sharing can be implemented as a series of pixel shuffling (reshape) operations and vanilla convolutions in a lower-resolution space. This network can now implement a wider range of behaviours, in particular it can implement something closer to the Bayes-optimal inference function.